Johann N. Löfflmann
Welcome to my private homepage
BigAl 2.4.0
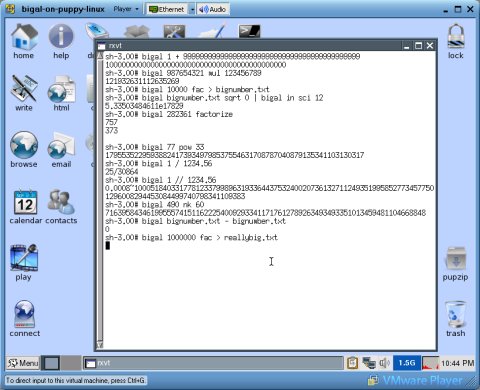
The screenshot above shows BigAl 2.4.0 in action on Puppy Linux 2.16.1 running in VMware Player for a time consuming "stop and continue" calculation.
Description
BigAl is a syntetic word made of "Big Algorithms". With BigAl you can calculate really BIG numbers with an accuracy your desktop calculator is still dreaming of. The only restriction is the power of your computer!Not only basic calculations are supported, but also special functions like factorial, fibonacci, lucas-sequence, periods, fraction reducing, square root, nth root, generation of random numbers, sum of the digits, binomial coefficient calculation, factorize function, bit oriented functions and many more. BigAl is able to handle numbers stored in files since Version 1.0. BigAl can also be used to simulate a high load on your computer.
BigAl is a free and open source software. BigAl is written entirely in Java, it runs on any platform that has a Java Runtime Environment. BigAl uses the Java classes called BigInteger and BigDecimal.
Here are some examples and a short description of the usage to demonstrate the program.
License
BigAl v2.4.0 Copyright © 2001-2012 Dipl.-Inf. (FH) Johann Nepomuk LöfflmannFor release notes click here.
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. See also FAQ.
Requirements
In order to run
BigAl, you need a Java Runtime Environment (JRE).
You can get it for free. It is required to have at least the JRE
version
1.4.2, but it is recommended to install JRE 6 or later.
Download
Read the Copyright. You have to read and accept the GNU General Public Licence if you want to use BigAl. Download
BigAl (version 2.4.0, June 23, 2007)
Filename:
bigal-2.4.0.zip
Filename:
bigal-2.4.0-on-puppy-linux-2.16.1.zip
Filename:
bigal-2.4.0-on-puppy-linux-3.01-in-virtualbox.zip
|
Acknowledgement: Barry Kauler is the
original developer and current
maintainer of Puppy Linux (http://www.puppylinux.com).
Note: Install instructions on How
to Install Puppy Linux on VMware und How
to Install Puppy Linux in a Virtualbox are available.
To verify the MD5 and the SHA digests, you can use the free
program
called Jacksum.
Read the readme.txt, stored in the file zip file to get useful
information
how to install the program on your computer.
Contact
Keep updated - the announcement-mail-alias:
Are you interested in hearing the latest from BigAl? If so, it is easy
to stay informed. Just subscribe to the announcement alias. It's just
only
me who can post messages to the list. Expect a maximum of 12 email per
year.
To subscribe to the list, send a message
to: announce-subscribe@bigal.java.net
To remove your address from the list, send a
message to:
announce-unsubscribe@bigal.java.net
View the announcements list archive: https://bigal.java.net/servlets/SummarizeList?listName=announce
Discuss with other users - the user-mail-alias:
If you have something for the wish list or if you have troulbe with
BigAl, write to this mailing list. The mailing list is a good place to
discuss new ideas, features and bugs.
To subscribe to the list, send a message
to: users-subscribe@bigal.java.net
To remove your address from the list, send a
message to:
users-unsubscribe@bigal.java.net
To write to the list, send a message to:
users@bigal.java.net
Trackers (Bug database, Support and Feature requests):
http://sourceforge.net/projects/bigal
Usage
Without any parameters you get this info| % bigal
BigAl v2.4.0, Copyright (C) 2001-2007, Dipl.-Inf. (FH) Johann N. Loefflmann BigAl
comes with ABSOLUTELY NO WARRANTY;
for details see 'license.txt'.
For
more information please type:
Fuer
weitere Informationen bitte eingeben:
|
Put the parameter "help" and you get a full description how
the program
can be used:
| % bigal
help
NAME
VERSION
SYNOPSIS
DESCRIPTION
The following parameters are supported: [help|-h] | <number|file|[std]in> <op> <number|file|[std]in> [?[?]]
help
this help
FUNCTIONS
A
eq
B equals?
A
abs|absolute
returns |A|
A
pow|^
N
power(A,N)
A and B are unlimited integer
variables
a
ack
B
ack(a,B) [Ackermann function]
Bit oriented, A and B are
unlimited integer variables
A
and
B
bit oriented AND
A
bcnt|bitcount
number
of bits that differ from its sign bit
EXAMPLES
Program
arguments
description
AUTHOR
LICENSE
This program is distributed
in the hope that it will be useful,
You should have received
a copy of the GNU General Public License
|
FAQ
Q: What does the % mean?A:
It is a standard Unix convention
to use % to represent the Unix command prompt (as
known as "shell").
If you see that sign, type everything behind it. It's also a standard
Windows
convention to use C:\> to represent the
Windows command prompt.
When you see a "prompt", type everything behind it.
Q: I get an error message by typing
| % bigal 3
* 4
invalid operation |
A: Usually, shells expands special characters like * to a filelist. Use the text operators (e. g. "mul") or mark it as a special character:
% bigal 3 \* 4
% bigal 3 "*" 4
C:\> java BigAl 3
"*" 4
C:\> java BigAl 3
mul 4
C:\> java BigAl 3 x
4
Q: Can I reduce a fraction?
A: Yes,
you can. Use the operation "div"
alias "/".
| % bigal 15
/ 145
3/29 |
Q: Can I process the output of a division further with BigAl?
A: Yes,
but you need to generate a normal
decimal number rather than a fraction.
| bigal 15
// 145 10
0.1034482759 |
______
Q: Is there a graphical
user interface for
BigAl ?
A: No. BigAl's purpose is to calculate with absolutely accuracy and it prefers to calculate with really big numbers. Those tasks are often very time consuming and it's possible that you don't get the result in a few minutes. It can take hours, days, weeks, month or even years until BigAl returns the result. Therefore, the commandline interface is the primary interface for BigAl. Let BigAl working in the background, redirect the output to files and do further processing with numbers stored in files.
Well, of course BigAl will help you also by solving simple tasks, but right now, also only at the command line.
Q: What purpose have the VMware image, respectively the VirtualBox?
A: The VMware Player respectively the VirtualBox are able to save the state of a Virtual Machine (VM). For the VMware Player select "Player -> Exit". For the VirtualBox select "Machine -> Close... -> Save the machine state". In order to restore the VM simply start the VM again.
As soon as the VM state has been restored, BigAl continues with the calculation. BigAl won't even recognize that there was a pause. Repeat the procedure as often as needed.
With this trick you can perform calculation tasks which take longer than only a few seconds or minutes. You can perform calculations which could take hours, days, months or even years if required, because you can interrupt a calculation at any time and you can continue a calculation whenever you want. You can even continue a calculation on a different computer!
Detailled descriptions can be found in the readme files which are included in the .zip file. Go to the download section. Do you want to see a screenshot?
Q: Can I use complex expressions with brackets?
A: No. Basically, only the simple expression <number> <operation> <number> is supported. But you can process the output of BigAl further with standard-input, pipes and files.
Q: Why is the following syntax not possible?
java -jar bigal.jar x + y > x
A: Your shell (or your command line interpreter) does not allow to do write to a file while you want to read from it. In other words, you cannot use the a file as output if it is part of one of the operators. What you can do is this:
java -jar bigal.jar x + y > zQ: I cannot enter very long numbers on the command line, what's wrong?
A: Your shell (or your command line interpreter) has a limit in accepting long strings, use a different shell (I recommend the bash on Linux/Unix) or store numbers in files. Numbers in files can be handled very well by BigAl.
Q: I get the error message called 'Exception in thread "main" java.lang.OutOfMemoryError: Java heap space'
A: The calculation you would like to perform requires more memory. You can increase the maximum heap space for the Java process with the option -Xmx. Example:
java -Xmx128m -jar bigal.jar
Examples
Task: 999999999999999999999999999999 + 6| % bigal
999999999999999999999999999999 +
6
1000000000000000000000000000005 |
If you would like to know how this number is called in words, use the NumericalChameleon.
Task: 123456789.987654321 *
987654321.123456789
| % bigal
123456789.987654321 * 987654321.123456789
=
121932632103337905.662094193112635269 |
Task: 4261655511456885005249781170177
34
| % bigal
4261655511456885005249781170177 div
34
125342809160496617801464152064, 1/34 |
To evaluate also the rest (1/34), use the operators called
"division"
or "//" rather than "div" or "/":
| % bigal
4261655511456885005249781170177 division
34
125342809160496617801464152064.0~2941176470588235 |
The "~" marks the beginning of the period. That means, the
result is
exactly:
________________
125342809160496617801464152064.02941176470588235
Task: What is the scientific representation of
12345.6789 ?
| % bigal
12345.6789 sci
1.23456789e4 |
=> the "scientific function" (sci) formats a normal number (12345.6789) to a scientific representation (1.23456789 * 104)
Task: What does the representation -12.34e-4 mean?
| % bigal
-12.34e-4 nop
-0.001234 |
=> the "no operation" (nop) formats a scientific representation (-12.34 * 10-4) to a normal number representation (-0.001234).
Task: fibonacci(100)
| % bigal
100 fib
354224848179261915075 |
Task: 100!
| % bigal
100 fac
93326215443944152681699238856266700490715968264381621468592963895217599993229915 608941463976156518286253697920827223758251185210916864000000000000000000000000 |
Note: the line break above (actually the number hasn't any line breaks) has been inserted by the terminal output.
Task: How long does it take to calculate 10000!
In this case, the result is unimportant, we redirect the
output to "/dev/null"
(use "nul" on Windows). It's saver to quote the question mark to avoid
any replacements by your shell.
| % bigal
10000 fac "?" > /dev/null
13450 |
The duration of the operation above was 13450 milliseconds. If
you want
it in format "day, hours, minutes, seconds, milliseconds" use "??"
rather
than "?".
| C:\>
bigal 10000 fac "??" > nul
0 d, 0 h, 0 m, 13 s, 589 ms |
Task: (100!)6
"in" or "stdin" are the names for BigAl's standard input
channel. Use
it with pipes ...
| % bigal 100 fac | java BigAl in pow 6 |
... or use numbers stored in files ...
| % bigal
100 fac > result.txt
% bigal result.txt pow 6 > endresult.txt |
The result of the task above is:
| 66072680842782571700144839317101301840126585582826215148182176376029419461561540
30965460940939195302947971311708312011730742707341761732940037569795738901145841 02473269764347820044961963433409159401386526300292515277729398331732374219968976 99619834464113022611312719240875831865184564835775630706232444860433123623379812 46320521788189559706361843657615135829382676759234804035064801643503656481020612 21954927504951861542739963712581629078497934366978856354573867875864286273108108 56212491608660094570046363549762087879009868883927677818940596991238387787187461 67935477457578759626212444254353125120437311719888665936989596855580234713843881 73909093242149941049935868447701664879408027118356453839078411480484971625514580 20383207512507640293499758197908132405790921327188236292549905069502719116940253 59360000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000 |
How many digits does the number have? Use the operation called
"length"
to get this info.
| % bigal
endresult.txt length
948 |
The example (100!)6 results in a number having 948 digits.
Task: 2^2^3That is the same as 2^8 and not 4^3. You must first calcualte the exponent and pass the result as being the next exponent. Use a pipe to pass the result to the next function.
| % bigal 2
pow 3 | bigal 2 pow in 256 |
Task: Factorize the number
44343535354351600000003434353
| % bigal
44343535354351600000003434353 factorize
149 329569479697 903019357561501 |
=> 149 * 329569479697 * 903019357561501 =
44343535354351600000003434353
All three numbers are primes.
Task: x * y by
entering x and y interactively
| % bigal in
mul in
3 4 12 |
Task: Is 98 an odd
or an even number?
| % bigal 98
getbit 0
0 |
Find out what bit 0 is (bit 0 is the least significant bit).
The result
0 means that the number 98 is even.
| % bigal 98
even
true |
Also the operator called "even", tells you that 98 is even.
Task: Get the
parity of a number
| % bigal 98
bitcount | bigal stdin getbit
0
1 |
3 bits are set in 98 (1100010) and 3 is an odd number. Therefore the result is 1.
How to calculate "the 9th root of the octal number 555760042152261557325705050700225 ?
I see. You want to know how old I am. :) Well, first you must convert the octal number to a decimal number.| % bigal 555760042152261557325705050700225 base 8 > decimal |
Then, calcualte the 9th root of the result (with zero decimal places)
| % bigal decimal rt 9 0 |
Factorial
Please note that the following table is correct since Nov 8, 2001. There were some typos before that date. Many thanks to Eugene G. Hamilton for this important hint. Don't panic, BigAl's factorial function works correctly since version 1.0.0 - there were only silly typos in the table below and not in the program.Here are the results from the factorial-function:
| n | factorial (n) |
| 10 | 3.6288 *106
(most human brains give up here already, try it: 1*2*3*4*5*6*7*8*9*10 = 3628800) |
| 70 | 1.197857166... * 10100
(most calculators fail here already) |
| 100 | 9.332621544... * 10157
(this is already more than one gogool) |
| 171 | 1.241018070... * 10309
(a few Javascript based Online-Programs give up at this stage) |
| 1000 | 4.023872600... * 102567 |
| 10000 | 2.846259680... *1035659 |
| 100000 | 2.824229407... *10456573 |
| 200000 | 1.420225345... *10973350 |
| 300000 | 1.477391531... *101512851 |
| 400000 | 2.534486046... *102067109 |
| 500000 | 1.022801584... *102632341 |
| 550000 | 6.073602851... *102918340 |
| 600000 | 2.234878177... *103206317 |
| 650000 | 3.750830256... *103496105 |
| 700000 | 6.491076229... *103787565 |
| 750000 | 2.646896442... *104080578 |
| 800000 | 5.684678740... *104375039 |
| 850000 | 1.383690070... *104670859 |
| 900000 | 3.990191093... *104967956 |
| 1000000 | 8.263931688...
*105565708
(a really nice large number - you need more than 5.5 million digits to write the number down) |
| 2000000 | 3.776821057...
* 1011733474
(it's bigger, 11 million digits, 11 MB are required to store the number uncompressed) |
| 3000000 | 9.038571657....
* 1018128483 (18.1 MB are required to store that number) |
| ... | ... |
Release Notes
Version 2.4.0 (Jun 23, 2007):- new operations
o support for the square root (sqrt) (sf# 1388680)
o support for the nth root (rt, root)
Thanks to Ronald Mark for the free source code
o support for converting a number from and to a numeral system
(base, tobase)
- improved operations:
o range and count parameters for the random function
o No parameter limits for the fibonacci/lucas function anymore
o No parameter limits for the factorial function anymore
o No parameter limits for the power function anymore and
performance improvement for power
o No parameter limits for the nk/choose function anymore
- support for the free cacaojvm
- JRE 1.4.2 or later required
- installer for Windows, build with NSIS v2.28
Version 2.3.1 (Jan 29, 2006):
- bugs fixed:
o since JRE 5.0 BigAl prints out scientific format
in some
cases, even if
we don't want sci format. This
change in BigDecimal's
toString() method
has been introduced by JSR 13.
BigAl works around
the documented
incompatibility to keep
compatibility with older
JVMs.
o ant script print warnings about non UTF-8
comments in
sourcecode
while compiling on Linux with
UTF-8 locale
- performance improvement for ackermann({0-4},n)
- BigAl 2.3.1 has been successfully tested with the Java
Runtime
Environments
gij 4.0.2, J2SE 1.3.1, J2SE 1.4.2, J2SE 5.0 and
Java SE
6.0-rc-b69
Version 2.3.0 (30-Apr-2005):
- BigAl has been successfully tested with the Java Runtime
Environments
Kaffe 1.1.4, gij 3.2.2, J2SE 1.3.1, J2SE 1.4.2,
J2SE 5.0
and J2SE 6.0-ea-b29
- bug fixed:
o information about the time needed for an
operation is
wrong
if the operation takes more
than 24 hours. Thanks
to
Stéphane Ecochard, France for
both the
bug report and the fix
o function divide throws OutOfMemoryException if
dividend
is negative
o function divide drops all digits after the comma
if divisor
is negative
o functions sod and len retrun wrong result if
value is
negative
- improved operations:
o Much faster Fibonacci function, provided by
Tobias Wahl,
Germany
o Floating point support for operations abs, add,
div, divide,
eq,
gt, ge, lt, le, mul, negate,
nop, round, sci,
signum, sub
- new operations:
o Factorize function (Pollard-Rho) from the
Princeton University
o Ackermann function provided by Tobias Braun,
Germany
o Random function to generate random numbers
o Round function for rounding numbers
o Sci function for formatting numbers in the
scientific
format
o Signum and Negate function
o Comparison functions eq, gt, ge, lt, le, odd and
even
- Unix/Linux-script and Windows-batch for being able to start
BigAl
easier
- System.exit() has been avoided, so BigAl can be used in
other
projects easier
- documentation updated
- with Ant build.xml file for developers
Version 2.2.0 (23-Feb-2002):
- improved fibonacci
(fixed an index problem, it is faster and can use
different
init values
for the lucas sequence for example)
- the factorial function gives now also a result for 0!
- new operations: abs, nk (very fast binomial coefficient
algorithm),
luc (lucas sequence)
- language support for english and german
- improved timer
- using J2SDK 1.3.1
- jar package, all you need is one jar file
Version 2.1.0a (08-Nov-2001):
- fixed some typos in the HTML
- still 2.1.0
Version 2.1.0 (25-Mar-2001):
- updated documentation
- new operations: length, getbit, setbit, flipbit, clearbit,
and, or, xor, not, bitcount, bitlength
Version 2.0.0 (11-Mar-2001):
- new operaion: nop (no operation)
- read values from standard input and from files
- duration of operations in ms and in d,h,m,s,ms on demand
- length of an operand on demand
- you can continue calculating factorial from a given value
- you can evaluate fractions with detailed period
Version 1.0.0 (25-Feb-2001):
- simple expression evaluation with unlimited numbers
- operations available: add, sub, mul, div, divide, mod, fib,
fac, pow, gcd, lcm, sod
