Johann N. Löfflmann • Informatiker
People rarely succeed until they have fun in what they are doing.
BigAl 2.4.0
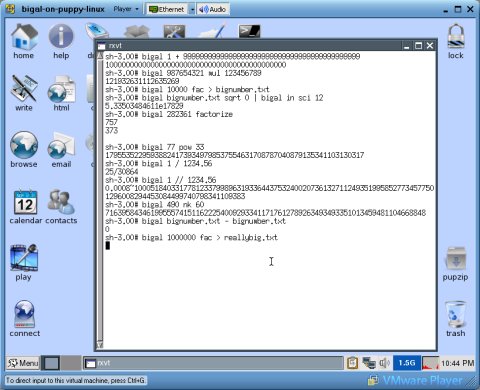
Das Bildschirmfoto zeigt BigAl in Aktion unter Puppy Linux 2.16.1, das im VMware Player läuft für eine zeitintensive "stop und weiter"- Berechnung.
Beschreibung
Mit BigAl können Sie SEHR GROSSE (und auch sehr kleine) Zahlen rechnen. Da Genauigkeit wichtig ist, werden Nachkommastellen standardmäßig nicht gerundet oder gekürzt. Egal wie groß oder klein ein Ergebnis sein wird, die einzigste Beschränkung ist die Leistungsfähigkeit Ihres Computers. Unterstützt werden neben den Grundrechenarten auch Funktionen wie Fakultät, Fibonacci, Lukas-Sequenz, exakte Periodenbestimmung bei Division, Kürzen von Brüchen, Quersummenberechnung, Bestimmung des Binomialkoeffizienten, Wurzelziehen, Generierung von Zufallszahlen und viele mehr.BigAl ist im Februar 2001 entstanden, weil ich wissen wollte, wieviel eine Million Fakultät nun ganz genau ist und eine Näherung eben nur eine Näherung ist. Ein paar Wochen Rechenzeit später erfuhr ich das Ergebnis. Wenn Sie ebenfalls von Zahlen begeistert sind und auch ein paar Antworten auf Ihre Fragen suchen, kann Ihnen BigAl evtl. auch nützliche Dienste erweisen. Deswegen stelle ich das komplette Programm unter die GPL, damit niemand das Rad neu erfinden muß. Natürlich hiflt Ihnen BigAl auch Zahlen im Bereich des natürlichen Lebens zu berechnen, BigAl's Stärken liegen aber definitiv im Micro- bzw. Macrobereich der Zahlen.
BigAl ist ein kostenloses, freies, plattformunabhängiges Programm. Es ist komplett in Java geschrieben und läuft auf allen Betriebssystemen, für die eine Java Laufzeitumgebung existiert (Windows, Linux, Unix, etc.). BigAl verwendet die Java-Klassen BigInteger und BigDecimal und es bevorzugt iterative statt rekursive Algorithmen.
Hier sind einige Beispiele und eine kurze
Beschreibung der Bedienung um die
Leistungsfähigkeit des Programm zu demonstrieren. BigAl kann auch nützlich
sein, um künstlich Last auf Ihrem Rechner zu erzeugen.
Lizenz
BigAl v2.4.0 Copyright (C) 2001-2012 Dipl.-Inf. (FH) Johann Nepomuk LoefflmannFür eine Programmhistorie klicken Sie bitte hier.

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 2 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details. See also FAQ.
Anforderungen
Um BigAl laufen zu lassen, benötigen Sie eine Java Laufzeitumgebung (JRE). Diese kann ebenfalls kostenlos heruntergeladen werden. Es ist mindestens die Version 1.4.2 erforderlich. Ich empfehle JRE 6 oder neuer.Download
Lesen Sie bitte vorher die Abschnitte Anforderungen und Copyright. Sie müssen den Bedingungen der GNU General Public Licence zustimmen, wenn Sie BigAl downloaden und benutzen möchten! Download (version 2.4.0 vom 23.06.2007) Download (version 2.4.0 vom 23.06.2007)
Filename: bigal-2.4.0.zip
Filename:
bigal-2.4.0-on-puppy-linux-2.16.1.zip
Filename:
bigal-2.4.0-on-puppy-linux-3.01-in-virtualbox.zip |
Würdigung: Barry Kauler ist der originale Entwickler und aktuelle
Maintainer von Puppy Linux (http://www.puppylinux.com).
Notiz: Installationsanweisungen How
to
Install Puppy Linux on VMware und How
to
Install Puppy Linux in a Virtualbox sind verfügbar.
Um die MD5 oder SHA Hashes zu überprüfen, verwenden Sie das freie
Programm Jacksum
Lesen Sie die Datei liesmich.txt, die Sie in der zip Datei finden. Sie
enthält nützliche Informationen zum Installieren von BigAl auf Ihrem
Computer.
Kontakt
Trackers (Bug database, Support and Feature requests):
https://sourceforge.net/projects/bigal
Bedienung
Ohne Parameter erhalten Sie folgende Info:| % java BigAl
BigAl v2.4.0, Copyright (C)
2001-2007 Dipl.-Inf. (FH) Johann N. Loefflmann
For more information please type:
Fuer weitere Informationen bitte
eingeben: |
Mit dem Parameter "hilfe" erhalten Sie eine vollständige Beschreibung der
Bedienung des Programms:
| % bigal hilfe NAME BigAl (Big Algorithms) VERSION SYNTAX: BESCHREIBUNG Die folgenden Parameter werden unterstuetzt: [hilfe] | <Zahl|Datei|[std]in> <Op> <Zahl|Datei|[std]in> [?[?]]
hilfe diese Hilfe FUNKTIONEN
A
eq
B Gleich (equals)?
A
abs
Gibt
den Absolutwert |A| zurueck
A
pow|^
N A hoch N (N ist
unbeschraenkte Ganzzahl) A und B sind
unbeschraenkte Ganzzahlen
a
ack
B Ackermann Funktion
(a,B) Bit orientiert, A
und B sind unbeschraenkte Ganzzahlen
A
and
B Bit orientiertes UND
A
bcnt|bitcount
Anzahl von Bits, untersch. vom Vz-Bit BEISPIELE
Programmargumente Beschreibung
AUTOR LIZENZ This program is
distributed in the hope that it will be useful,
You should have
received a copy of the GNU General Public License
|
FAQ
Q: Was bedeutet das $?A: Es ist eine Konvention unter
GNU/Linux und Unix, das $ Zeichen als Repräsentant für die
Eingabeaufforderung ("shell") zu verwenden. Lassen Sie dieses Zeichen bei
der Eingabe weg. Es ist auch eine Konvention unter Microsoft Windows die
Zeichen "C:\>" zu verwenden, um die Eingabeaufforderung unter
Windows zu repräsentieren. Lassen Sie auch diese Zeichen bei der Eingabe
einfach weg.
Q: Ich erhalte eine Fehlermeldung "invalid operation"
| $ java BigAl 3 * 4 invalid operation |
A: Üblicherweise interpretieren Shells (Kommandointerpreter) spezielle Zeichen wie den Stern (*) als Sonderzeichen. Um dies zu vermeiden, benutzen Sie stattdessen Textoperatoren (z. B. "mul") oder kennzeichnen Sie Sonderzeichen als solche:
$ bigal 3 \* 4
$ bigal 3 "*" 4
C:\> bigal 3 "*" 4
C:\> bigal 3 mul 4
C:\> bigal 3 x 4
Q: Kann ich einen Bruch kürzen?
A: Ja, benutzen Sie die Operation "div" oder
"/".
| $ java BigAl 15 / 145 3/29 |
Q: Kann ich die Ausgabe einer Division mit BigAl weiterverarbeiten?
A: Ja, aber Sie müssen eine normale
Dezimalzahl ausgeben lassen statt eines Bruches.
| $ bigal 15 // 145 10 0.1034482759 |
______
Q: Gibt es eine graphische Oberfläche für BigAl ?
A: Nein. Der Zweck von BigAl ist es, mit absoluter Genauigkeit bevorzugt möglichst große Zahlen zu berechnen. Solche Aufgaben sind oft sehr zeitintensiv und es ist möglich, daß Sie das Ergebnis einer aufwendigen Berechnung erst in ein paar Minuten, Stunden, Tagen, Wochen, Monaten oder sogar erst nach einigen Jahren erhalten. Deshalb ist die Kommandozeile das primäre Interface für BigAl. Lassen Sie BigAl im Hintergrund arbeiten und rechnen Sie mit Zahlen, die in Dateien gespeichert sind, lenken Sie die Ausgabe wieder in Dateien für weitere Berechnungen um, usw.
Natürlich hilft Ihnen BigAl auch bei der Lösung einfacher Rechenaufgaben, jedoch nur auf der Kommandozeile.
Q: Wozu ist das VMware image bzw. die VirtualBox gut?
A: Der VMware Player, bzw. die VirtualBox sind in der Lage, den Status der Virtuellen Maschine (VM) zu sichern. Für den VMware Player wählen Sie "Player -> Exit", für die VirtualBox wählen Sie "Machine -> Close... -> Save the machine state". Um die VM wiederherzustellen, starten Sie einfach die VM erneut.
Sobald der gespeicherte Status der VM wiederhergestellt wurde, fährt BigAl mit der unterbrochenen Berechnung fort. BigAl wird nicht einmal merken, daß es eine Pause gab. Wiederholen Sie die Prozedur so oft wie nötig.
Mit diesem Trick können Sie Berechnungen durchführen, die länger als nur ein paar Sekunden oder Minuten dauern. Sie können Berechnungen durchführen, die Stunden, Tage, Monate oder sogar Jahre benötigen können, da Sie die Berechnung jederzeit unterbrechen und später wieder fortsetzen können, wann immer Sie es möchten. Sie können sogar eine Berechnung auf einem anderen/neueren Computer fortsetzen, wenn Sie die VM transferrieren.
Eine ausführliche Beschreibung finden Sie in den readme-Dateien, die in der .zip-Datei gespeichert sind. Gehen Sie zur Download Sektion. Möchten Sie ein Bildschirmfoto sehen?
Q: Kann ich komplexe Ausdrücke mit Klammern benutzen?
A: Nein. Nur der einfache Ausdruck <Zahl> <Operation> <Zahl> wird z. Zt. unterstützt. Sie können die Ausgabe von BigAl jedoch über den Pipemechanismus oder Dateien weiterverarbeiten.
Q: Warum ist die folgende Syntax nicht möglich?
java -jar bigal.jar x + y > x
A: Ihre Shell (bzw. Ihr Kommandozeileninterpreter) erlaubt es nicht in eine Datei zu schreiben, während von der gleichen Datei gelesen wird. Mit anderen Worten, man kann nicht in eine als Operator benutzte Datei schreiben.
Q: Ich kann keine sehr langen Zahlen auf der Kommandozeile schreiben, warum?
A: Ihre Shell (bzw. Ihr Kommandozeileninterpreter) hat ein Limit für Zeichenketten. Verwenden Sie eine andere Shell (für GNU/Linux und Unix Systeme empfehle ich die bash) oder speichern Sie die Zahlen in Dateien. In Dateien gepsicherte Zahlen können von BigAl verarbeitet werden.
Q: Ich erhalte die Fehlermeldung 'Exception in thread "main" java.lang.OutOfMemoryError: Java heap space'
A: Die Berechnung, die Sie durchführen möchten, benötigt mehr Speicher. Sie können dem Java Prozess mehr Speicher zuweisen, indem Sie den Maximalwert erhöhen, der für den Java Heap zur Verfügung stehen darf. Das geht mit der Option -Xmx. Beispiel:
java -Xmx512m -jar bigal.jar
Sollten Sie ein 64 bit Betriebssystem fahren, beachten Sie, dass Sie auch eine 64 bit Java Laufzeitumgebung benötigen, um mehr als 4 GB (in der Praxis tatsächlich mehr als etwa 2,5 GB bis 3 GB, abhängig vom Betriebssystem) für den maximalen Java Heap Space zu spezifizieren.
Beispiele
Aufgabe: 999999999999999999999999999999 + 6| $ java BigAl
999999999999999999999999999999 + 6 1000000000000000000000000000005 |
Wenn Sie erfahren möchten, wie diese Zahl ausgesprochen wird, verwenden Sie das freie Programm NumericalChameleon.
Aufgabe: 123456789.987654321 * 987654321.123456789
| $ bigal 123456789.987654321 *
987654321.123456789 = 121932632103337905.662094193112635269 |
Aufgabe: 4261655511456885005249781170177
34
| $ bigal
4261655511456885005249781170177 div 34 125342809160496617801464152064, 1/34 |
um den Rest (1/34) auszuwerten, benutzen Sie bitte die Operatoren
"division" oder "//" statt "div" oder "/":
| $ bigal
4261655511456885005249781170177 division 34 125342809160496617801464152064.0~2941176470588235 |
Die Tilde ("~") kennzeichnet den Beginn der Periode. Das bedeutet, das
Ergebnis ist exakt::
________________
125342809160496617801464152064.02941176470588235
Aufgabe: Wie lautet die wissenschaftliche Anzeige von 12345.6789 ?
| $ bigal 12345.6789 sci 1.23456789e4 |
=> die Funktion "scientific" (sci) formatiert die Dezimalzahl (12345.6789) in die wissenschaftliche Repräsentierung (1.23456789 * 104)
Aufgabe: Was bedeutet die Zahl -12.34e-4 ?
| $ bigal -12.34e-4 nop -0.001234 |
=> die Funktion "no operation" (nop) formatiert die wissenschaftliche Repräsentierung (-12.34 * 10-4) in eine normale Dezimalzahl (-0.001234).
Aufgabe: fibonacci(100)
| $ bigal 100 fib 354224848179261915075 |
Aufgabe: 100!
| $ bigal 100 fac 93326215443944152681699238856266700490715968264381621468592963895217599993229915 608941463976156518286253697920827223758251185210916864000000000000000000000000 |
Aufgabe: Wie lange benötigt die Berechnung von 10000!
In der gestellten Aufgabe ist das Ergebnis erstmal irrelevant. Wir geben
die Ausgabe des Wertes auf "/dev/null" ("nul" unter Windows). Es ist
sicherer, das Fragezeichen in Gänsefüßchen zu setzen, um eine automatische
Ersetzung durch die Shell zu vermeiden.
| $ bigal 10000 fac "?" > /dev/null
13450 |
Die Dauer der Operation war 13450 Millisekunden. Wenn Sie die Ausgabe
lieber in der Form "Tage, Stunden, Minuten, Sekunden, Millisekunden" haben
wollen, benutzen Sie "??" statt "?".
| C:\> bigal 10000 fac ?? > nul
0 d, 0 h, 0 m, 13 s, 589 ms |
Aufgabe: (100!)6
"in" oder "stdin" ist die Bezeichnung für BigAl für die Standardeingabe.
Sie können sie mit Pipes verknüpfen ...
| $ bigal 100 fac | java BigAl in pow 6 |
... oder Sie benutzen einfach Zahlen in Dateien ...
| $ bigal 100 fac > result.txt
$ bigal result.txt pow 6 > endresult.txt |
Das Ergebnis der obigen Aufgabe ist übrigens:
| 66072680842782571700144839317101301840126585582826215148182176376029419461561540
30965460940939195302947971311708312011730742707341761732940037569795738901145841 02473269764347820044961963433409159401386526300292515277729398331732374219968976 99619834464113022611312719240875831865184564835775630706232444860433123623379812 46320521788189559706361843657615135829382676759234804035064801643503656481020612 21954927504951861542739963712581629078497934366978856354573867875864286273108108 56212491608660094570046363549762087879009868883927677818940596991238387787187461 67935477457578759626212444254353125120437311719888665936989596855580234713843881 73909093242149941049935868447701664879408027118356453839078411480484971625514580 20383207512507640293499758197908132405790921327188236292549905069502719116940253 59360000000000000000000000000000000000000000000000000000000000000000000000000000 00000000000000000000000000000000000000000000000000000000000000000000 |
Wie viele Ziffern? Benutzen Sie die Operation "length" um diese
Information zu erhalten.
| $ bigal endresult.txt length
948 |
Aufgabe: 2^2^3
Bitte beachten: das ist das gleiche wie 2^8 und nicht 4^3. Zuerst muss der letzte Exponent berechnet werden (also 2^3), dessen Ergebnis dann der Exponent für die tieferliegende Funktion wird. Mit BigAl wird das Ergebnis einfach per Pipe an die nächste Funktion übergeben.
| $ bigal 2 pow 3 | bigal 2 pow in 256 |
Aufgabe: Faktorisieren Sie die Zahl 44343535354351600000003434353
| $ bigal 44343535354351600000003434353
factorize 149 329569479697 903019357561501 |
=> 149 * 329569479697 * 903019357561501 =
44343535354351600000003434353
Alle drei Zahlen sind Primzahlen, weil sie nicht weiter zerlegt werden
können.
Aufgabe: x * y bei Eingabe von x und y über die
Tastatur
| $ bigal in mul in 3 4 12 |
Aufgabe: ungerade oder gerade Zahl?
| $ bigal 98 getbit 0 0 |
Es genügt, herauszufinden welchen Wert Bit 0 besitzt (least significant
bit ist rechts). Das Ergebnis 0 bedeutet, die Zahl 98 is also gerade.
| $ bigal 98 even true |
Auch der Operator "even" ermittelt, daß es sich um eine gerade Zahl handelt.
Aufgabe: Parität einer Zahl
| $ bigal 98 bitcount | java BigAl stdin
getbit 0 1 |
3 Bits sind gesetzt in 98 (1100010) und 3 ist eine ungerade Zahl, weil
das "lest significant bit" in der Binärdarstellung von 3 eine 1 ist. In
anderen Worten, 98 muss gerade sein.
Fakultät
Die folgende Liste ist seit dem 08.11.2002 korrekt. Vor diesem Datum enthielt die Tabelle einige Tippfehler. Dank gilt Eugene G. Hamilton für diesen wichtigen Hinweis. Bitte beachten Sie, dass BigAl seit der Version 1.0.0 korrekt rechnet - die Fehler waren nur in der Tabelle und nicht im Programm.Hier sind die Ergebnisse der Funktion Fakultät:
| n | Fakultät (n) |
| 10 | 3.6288 *106 (die meisten menschlichen Gehirne geben hier bereits auf, versuchen Sie's: 1*2*3*4*5*6*7*8*9*10 = 3628800) |
| 70 | 1.197857166... * 10100 (die meisten handelsüblichen Taschenrechner geben hier bereits auf) |
| 100 | 9.332621544... * 10157 (das ist schon mehr als ein Gogool) |
| 104 | 1.029901674... * 10166 (der Taschenrechner auf dem Apple iPhone 3GS (iOS 6) gibt hier auf) |
| 171 | 1.241018070... * 10309 (einige Javascript basierte Online-Programme geben hier auf) |
| 1000 | 4.023872600... * 102567 |
| 3249 | 6.412337688.. * 1010000 (der Taschenrechner von Windows 10 gibt hier auf mit einem Überlauf) |
| 10000 | 2.846259680... *1035659 |
| 100000 | 2.824229407... *10456573 |
| 200000 | 1.420225345... *10973350 |
| 300000 | 1.477391531... *101512851 |
| 400000 | 2.534486046... *102067109 |
| 500000 | 1.022801584... *102632341 |
| 550000 | 6.073602851... *102918340 |
| 600000 | 2.234878177... *103206317 |
| 650000 | 3.750830256... *103496105 |
| 700000 | 6.491076229... *103787565 |
| 750000 | 2.646896442... *104080578 |
| 800000 | 5.684678740... *104375039 |
| 850000 | 1.383690070... *104670859 |
| 900000 | 3.990191093... *104967956 |
| 1000000 | 8.263931688... *105565708 (eine schöne große Zahl - man benötigt über 5,5 Millionen Ziffern, um sie komplett niederzuschreiben) |
| 2000000 | 3.776821057... * 1011733474 (noch ein wenig größer - 11 Millionen Ziffern oder 11 MB um die Zahl unkomprimiert zu speichern) |
| 3000000 | 9.038571657.... * 1018128483 (18.1 MB sind erforderlich, um die Zahl unkomprimiert zu speichern) |
| ... | ... |
Historie
Version 2.4.0 (Jun 23, 2007):- new operations
o support for the square root (sqrt) (sf# 1388680)
o support for the nth root (rt, root)
Thanks to Ronald Mark for the free source code
o support for converting a number from and to a numeral system
(base, tobase)
- improved operations:
o range and count parameters for the random function
o No parameter limits for the fibonacci/lucas function anymore
o No parameter limits for the factorial function anymore
o No parameter limits for the power function anymore and
performance improvement for power
o No parameter limits for the nk/choose function anymore
- support for the free cacaojvm
- JRE 1.4.2 or later required
- installer for Windows, build with NSIS v2.28
Version 2.3.1 (Jan 29, 2006):
- bugs fixed:
o since JRE 5.0 BigAl prints out scientific format in some
cases, even if
we don't want sci format. This change in
BigDecimal's toString() method
has been introduced by JSR 13. BigAl works around
the documented
incompatibility to keep compatibility with older
JVMs.
o ant script print warnings about non UTF-8 comments in
sourcecode
while compiling on Linux with UTF-8 locale
- performance improvement for ackermann({0-4},n)
- BigAl 2.3.1 has been successfully tested with the Java Runtime
Environments
gij 4.0.2, J2SE 1.3.1, J2SE 1.4.2, J2SE 5.0 and Java SE
6.0-rc-b69
Version 2.3.0 (30-Apr-2005):
- BigAl has been successfully tested with the Java Runtime
Environments
Kaffe 1.1.4, gij 3.2.2, J2SE 1.3.1, J2SE 1.4.2, J2SE 5.0 and
J2SE 6.0-ea-b29
- bug fixed:
o information about the time needed for an operation is wrong
if the operation takes more than 24 hours. Thanks
to
Stéphane Ecochard, France for both the bug report
and the fix
o function divide throws OutOfMemoryException if dividend is
negative
o function divide drops all digits after the comma if divisor
is negative
o functions sod and len retrun wrong result if value is
negative
- improved operations:
o Much faster Fibonacci function, provided by Tobias Wahl,
Germany
o Floating point support for operations abs, add, div, divide,
eq,
gt, ge, lt, le, mul, negate, nop, round, sci,
signum, sub
- new operations:
o Factorize function (Pollard-Rho) from the Princeton
University
o Ackermann function provided by Tobias Braun, Germany
o Random function to generate random numbers
o Round function for rounding numbers
o Sci function for formatting numbers in the scientific format
o Signum and Negate function
o Comparison functions eq, gt, ge, lt, le, odd and even
- Unix/Linux-script and Windows-batch for being able to start BigAl
easier
- System.exit() has been avoided, so BigAl can be used in other
projects easier
- documentation updated
- with Ant build.xml file for developers
Version 2.2.0 (23-Feb-2002):
- improved fibonacci
(fixed an index problem, faster and can use different init
values
for the lucas sequence for example)
- factorial gives now also a result for 0!
- new operations: abs, nk (very fast binomial coefficient algorithm),
luc (lucas sequence)
- language support for english and german
- improved timer
- using J2SDK 1.3.1
- jar package, all you need is one jar file
Version 2.1.0a (08-Nov-2001):
- fixed some typos in the HTML
- still 2.1.0
Version 2.1.0 (25-Mar-2001):
- updated documentation
- new operations: length, getbit, setbit, flipbit, clearbit,
and, or, xor, not, bitcount, bitlength
Version 2.0.0 (11-Mar-2001):
- new operaion: nop (no operation)
- read values from standard input and from files
- duration of operations in ms and in d,h,m,s,ms on demand
- length of an operand on demand
- you can continue calculating factorial from a given value
- you can evaluate fractions with detailed period
Version 1.0.0 (25-Feb-2001):
- simple expression evaluation with unlimited numbers
- operations available: add, sub, mul, div, divide, mod, fib,
fac, pow, gcd, lcm, sod
